It’s one of the most annoying things ever (#FirstWorldProblems): a wobbly table. And no matter how hard you try, putting bits of paper or cardboard coasters under one of the legs, tightening screws, or just giving up and eating on the floor, you’ll never be left satisfied.
Till now.
In comes math – the solution to (almost) everything!
The Mathematical Solution to the Wobbly Table
As with many things in math, we start by making some assumptions. Let’s imagine your sitting at a 4-legged table that is really well made – so the legs are actually equal in length. You are, however, sitting on some pretty uneven ground, your table is very wobbly and has already caused you to spill your coffee.
You’ve tried putting a bit of paper under the table, maybe a paper coaster. For a while, this works. But eventually, the paper gets compressed and you’re back to wobbling.
But there is a solution: just turn (not flip!) the table! Somewhere on the way to a 90-degree turn, you’ll find an equilibrium!
I know, it sounds unbelievable. Magical even. But there is math to back it all up!
Consider the height of leg number 1 (the unstable one) off the floor as h. At the start of your struggles, this height is larger than one (because it’s off the floor, remember!), so h(t=0) > 0.
While turning the table 90 degrees, at some point that leg would move “under” the surface of the floor, if it could. So at some point h(t) < 0.
There a mathematical theorem that we can now turn to for help: the mean value theorem. This states that if you have a continuous function that is positive on one end, and negative on the other, there must be (at least) one zero value! This makes total sense if you think about it: to get from A (positive) to B (negative) in a continuous manner, you’ll have to pass through zero!
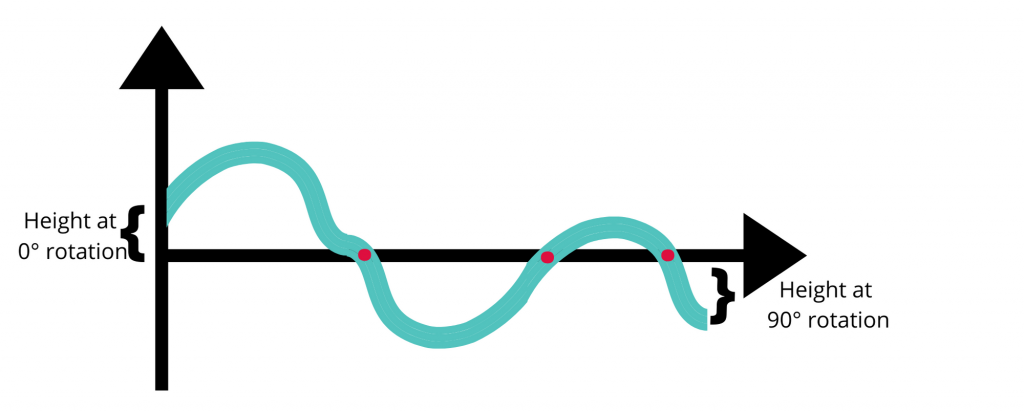
Of course “Mathematics is all theoretical”. Theoretically, turning the table will unwobble your table but there are many situations where it might not work: maybe your table isn’t perfectly square, or does not have four legs, or cannot be moved.
In that case:
“If you can’t move the table, you’ll have to use the paper trick.”
Good ol’ reliable paper.
Source:
https://arxiv.org/pdf/math-ph/0510065v6.pdf
Watch the explanation here:

