“It was octarine, the colour of magic. It was alive and glowing and vibrant and it was the undisputed pigment of the imagination, because wherever it appeared it was a sign that mere matter was a servant of the powers of the magical mind. It was enchantment itself.
― Terry Pratchett, The Color of Magic
But Rincewind always thought it looked a sort of greenish-purple.”
I’ve always imagined octarine to be that green-purple metallic color of bird feathers. You know, that color that seems to change depending on the incidence of light?

Just humming outside our window
We have a plant outside our window. It has tiny yellow flowers that bloom in the winter and seem like they taste delicious. Or would taste delicious if I were a hummingbird.

We have at least two regular hummy-visitors, that I’ve seen. Just buzzing around just outside our window, usually, when I’m on a phone call and I lose my train of thought and end up sounding (even more) incoherent on my call.
In my defense, I grew up in a place where hummingbirds aren’t that common, so they are pretty amazing for me to see.
Hummingbirds are amazing. They are the only birds that can fly not only backward, but also upside down. They are tiny, and weigh almost nothing; the average ruby-throated hummingbird weighs about 3 grams (one-tenth of an ounce), which is about the weight same as a penny! Some species can fly for up to 22 hours non-stop during their migration over the Gulf of Mexico. And a flock of hummingbirds is called either a bouquet, a glittering, a hover, a shimmer, or a tune – which is just beautiful.
But, I think the most fascinating part is how their color seems to change. From one angle, one of the two birds has a deep red colored throat. Change the angle slightly, and it looks completely different.
What bird are we seeing?
First things first, there are over 330 hummingbird species worldwide, at least 23 types in North America and – we’re narrowing things down – 6 commonly found in the region we live, the Pacific North West.
Considering we’re seeing these tiniest of birds in the winter, and there are only one species that don’t migrate south for the winter, we are probably seeing Anna’s Hummingbird (Calypte anna), named after Anna Masséna the wife of a nineteenth-century bird collector.
Male Anna’s Hummingbirds have a brightly colored neck. There are about 1.5 million of these hummingbirds in existence. They are quite common, and seemed to have adapted well to urban environments – they surely don’t seem to mind buzzing outside our window and distracting me from phonecalls!
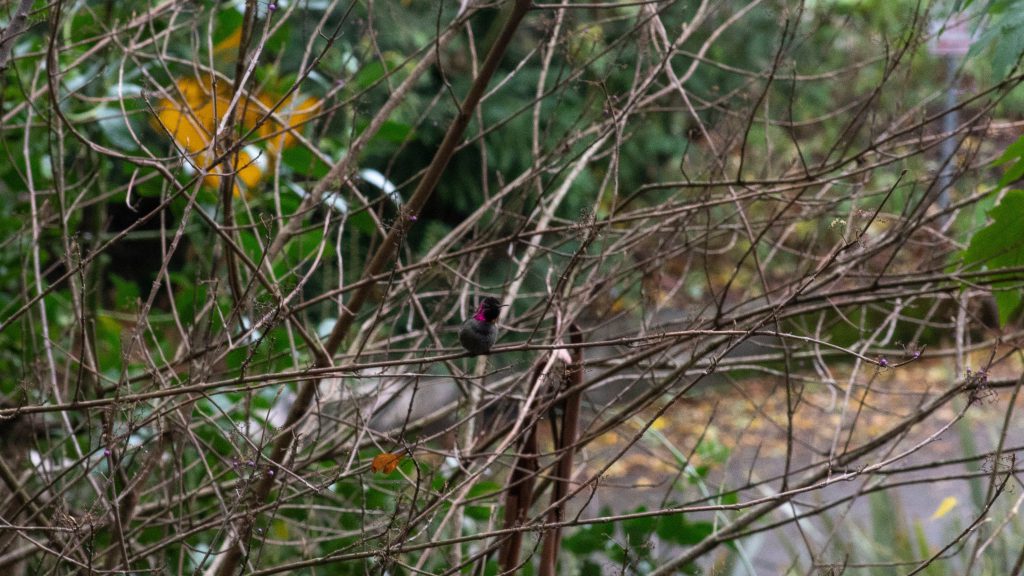
Why do hummingbird feathers (seem to) change color?
Hummingbird feathers aren’t “the color of magic,” they show the optical phenomenon called iridescence. Iridescent surfaces seemingly change color depending on the view or illumination angle. It’s the same effect that causes that rainbow sheen on a soap bubble, that lenticular-looking effect on some minerals, the changing colors of the tapetum lucidum, and that metallic shine on butterflies and bird wings.
The colors of the material are not due to a pigment (though that can determine the base color), but due to microstructures within the material that interfere with light in different ways (structural coloration).
Structural coloration: reflection, refraction, interference
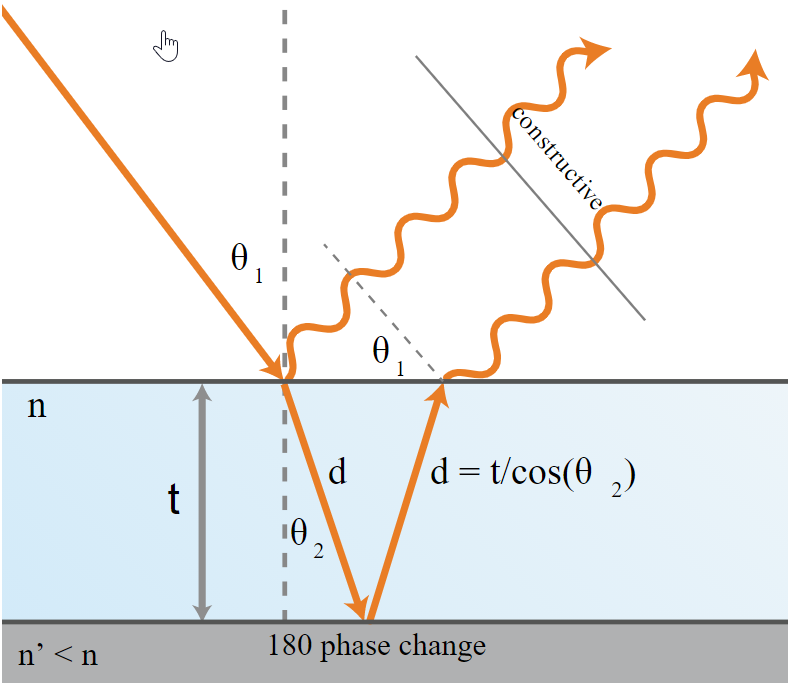
Let’s take the example of a soap bubble. A soap bubble can be considered a thin film, it basically has two interfaces: the air-soap interface, and the soap-water interface. Light will interact with those interfaces in two ways: some light will be reflected (like on a mirror), and some will transmit and refract (change of angle due to material change).
So if we consider a single incoming ray of light, it will be reflected twice, once at each interface – and two rays will interact with each other by interference. Constructive interference happens when the light is in phase, destructive when it’s out of phase.
Depending on the angle of the incoming light, the angle of where we observe the light, the thickness of the film, etc. certain wavelengths (or colors) will be visible to the observer, because the rays constructively interfere, while others colors will be cancelled out.
This phenomenon is called thin-film interference, an effect that occurs when the material thickness is of the same order as the wavelength of visible light (380-750 nm).
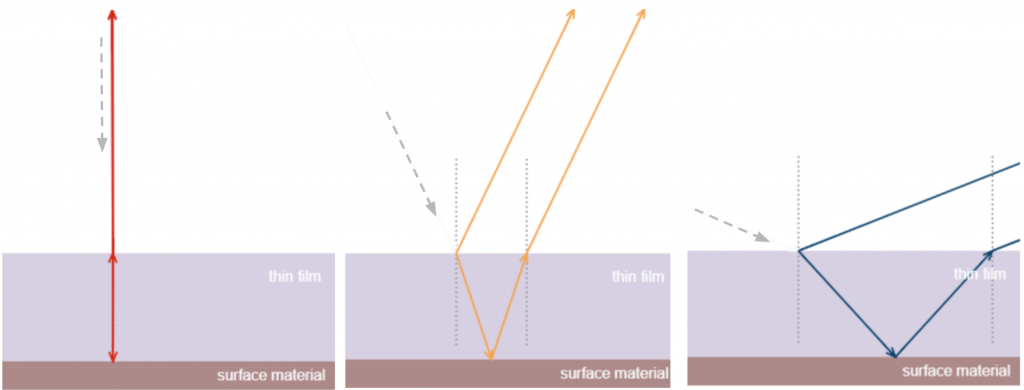
Changing angles
When we change the angle of incoming light (by changing from which angle we observe), the thickness through which the light has to travel changes, changing its interference pattern. For example, looking straight on might make the film look red, while at an angle the same material will look orange or green or blue. This is how we see a rainbow effect on a soap bubble.
A lot of tiny little mirrors
The same thing happens when we have certain crystalline structures, which is why some minerals show iridescence, or materials that are basically just a bunch of tiny little mirrors (like CDs).
The same is true for bird feathers, they show a regular crystalline nanostructure: individual tiny mirrors are spaced out just right to cause constructive interference of certain colors at a certain wavelength. And that’s why the Anna’s Hummingbird that chills* out outside our window sometimes looks like he has a bright Fuschia neck, and sometimes he does not.

From Parry, Ahu & Savin, Thierry. (2016). Recent advances in the biomimicry of structural colours. Chem. Soc. Rev.. 45. 10.1039/C6CS00129G.
Anyway, to me, octarine is real, and not only on Discworld.
*Actually, I’m not sure hummingbirds now how to “chill.”

