Category: Science History

[…] of the construction and growth and working of the body, as of all else that is of the earth earthy, physical science is, in my humble opinion, our only teacher and guide. (1)

You might have seen the xkdc comic ranking different scientific disciplines by their purity (and if you haven’t, it’s just a bit of scrolling away). The idea it portrays is that all sciences are basically applied physics (which is in turn applied mathematics). In other words: if you go deep enough to a subject, you eventually end up explaining in with principles from physics. And this is the same principle D’Arcy explores in his book. That has over 1000 pages, did you know that?

A famous D’Arcy quote states that the study of numerical and structural parameters are the key to understanding the Universe:

I know that the study of material things number, order and position are the threefold clue to exact knowledge, and that these three, in the mathematician’s hands, furnish the ‘first outlines for a sketch of the Universe.’ (2)

You can ask the average high school student about mathematics, and the usual response would probably be something in the lines of: “Ugh, I’ll never use this for anything.” Sometimes, it might be difficult to see the every-day use of mathematics, or even the not-so-everyday use. But in reality, the possibilities are endless (given that we are open to having long lists of endless equations that need a supercomputer to solve – probably).

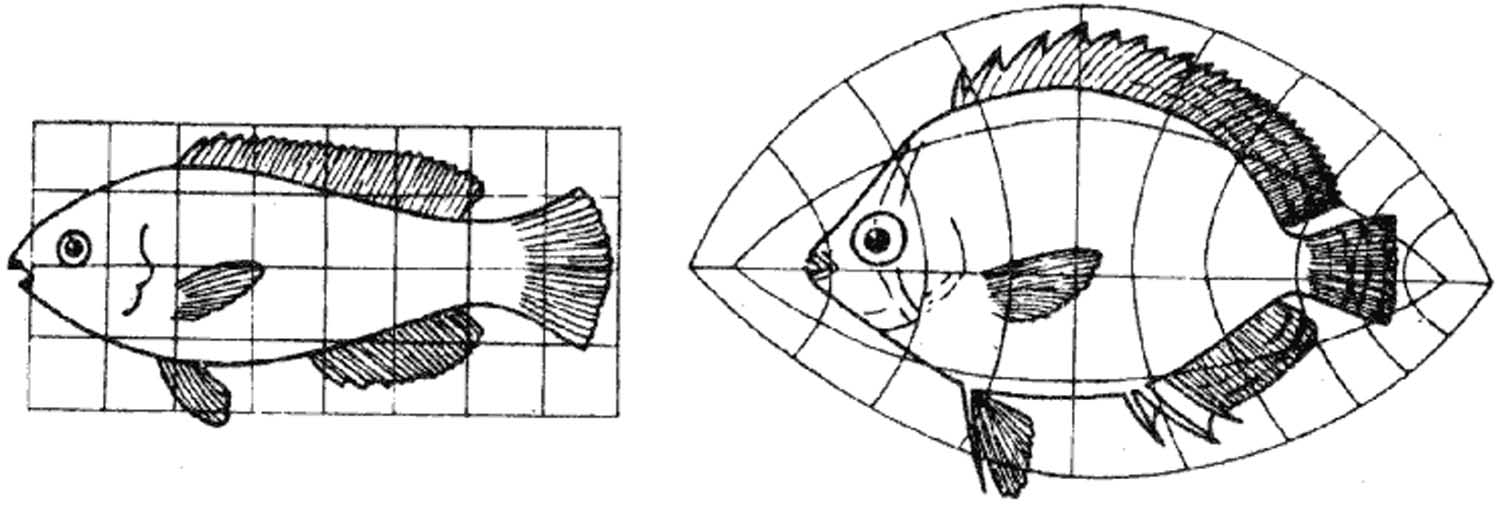
We are apt to think of mathematical definitions as too strict and rigid for common use, but their rigour is combined with all but endless freedom. The precise definition of an ellipse introduces us to all the ellipses in the world; the definition of a ‘conic section’ enlarges our concept, and a ‘curve of higher order’ all the more extends our range of freedom.

It might not be straightforward to see how mathematics (or physics for that matter) would help a biologist in the understanding of natural processes. However, there are a few examples of how physical properties, forces or phenomena are used in biology, such as helping bone repair:

The soles of our boots wear thin, but the soles of our feet grow thick the more we walk upon them: for it would seem that the living cells are “stimulated” by pressure, or by what we call “exercise,” to increase and multiply. The surgeon knows, when he bandages a broken limb, that his bandage is doing something more than merely keeping the part together: and that the even, constant pressure which he skilfully applies is a direct encouragement of the growth and an active agent in the process of repair. (4)

Nowadays the link between physics and biology is more accepted that a century ago, leading to new research fields such as biomechanics, mechanobiology and “physics of cancer”. I have eluded to some of the links between cancer and physics in previous posts (Physics of Cancer, Part I and II). Mathematical models are commonly used to better understand biological processes, including signalling pathways, tissue formation and growth and changes occurring in cancer.

This goes to show (again) that “interdisciplinary” is not just a fancy buzzword, it is a core principle of scientific research. While I must admit from own experience that carrying out interdisciplinary research might not be the easiest path, the potential discoveries and applications are even more endless. And while it might seem mind-boggling, I would argue that mind-bogglement is a good thing, stretching the potential of our minds and our understanding of the universe. And as far as I can read, D’Arcy agrees:

… if you dream, as some of you, I doubt not, have a right to dream, of future discoveries and inventions, let me tell you that the fertile field of discovery lies for the most part on those borderlands where one science meets another. There is a cry in the land for specialisation … but depend on it, that the specialist who is not reinforced by a breadth of knowledge beyond his own speciality is apt very soon to find himself only the highly trained assistant to some other man … Try also to understand that though the sciences are defined from one another in books, there runs through them all what philosophers used to call the commune vinculum, a golden interweaving link, to their mutual support and interpretation. (5)

So I guess my point is (if there even was a point in this post, apart from that the book has like over 1000 pages, in case you didn’t know): if you are a biologist, don’t be afraid to break some sweat and get physical. And the opposite goes for physicists. You might want to get a bit chemical as well, while you’re at it.

The Homo Universalis is back!

---

(1) On Growth and Form, p 13.

(2) On Growth and Form, p. 1096
(3) On Growth and Form, p. 1027
(4) On Growth and Form, p. 985
(5) D’Arcy Thompson and his zoology museum in Dundee – booklet by Matthew Jarron and Cathy Caudwell, 2015 reprint
(1-4) from D’Arcy Thompson, On Growth and Form,  Cambridge university press, 1992 (unaltered from 1942 edition)

Ever since I have been enquiring into the works of Nature I have always loved and admired the Simplicity of her Ways. (1)

In his book (yes, it’s about that again), D’Arcy supports his ideas through examples, through observations on biological systems that he can either explain through mathematical equations or directly compare to purely physical phenomena such as bubble formation. You might think that these are grave simplifications.

However, even in biology, which some people might call a “complex science”, simplifications are often used. Using cell culture rather than tissue. Isolating a single player in a pathway to see what its effect is. And quite often, a simplification holds true within the limits that have been set up to define it.

As was pointed out to me recently, the definition of “complex” is that something is “composed of many interconnected parts”. Meaning that this is not necessarily the antonym to “simple”. But “complex” is often seen to mean the same thing as “difficult”, even if that’s not necessarily the definition. In any case, it is definitely not so that physics is a “simple science”:

But even the ordinary laws of the physical forces are by no means simple and plain. (2)

It makes sense to break down a complex system into its individual components and analyse these, perhaps more simple concepts, separately. There is great value in simplifying things. First of all, there is a certain beauty in simplicity:

Very great and wonderful things are done by means of a mechanism (whether natural or artificial) of extreme simplicity. A pool of water, by virtue of its surface, is an admirable mechanism for the making of waves; with a lump of ice in it, it becomes an efficient and self-contained mechanism for the making of currents. Music itself is made of simple things – a reed, a pipe, a string. The great cosmic mechanisms are stupendous in their simplicity; and, in point of fact, every great or little aggregate of heterogeneous matter involves, ipso facto, the essentials of a mechanism. (3)

When reading this paragraph, two things jumped out at me. Two weeks ago, I was at the annual meeting of the British Society for Cell Biology (joint with other associations) and heard an interesting talk by Manuel Théry. Part of his story relied on putting boundaries on a system. Without boundaries, whatever we would like to study just gets too complicated, and we are unable to understand what is happening. For example, when explaining how waves originate, it is much easier to use a system where water is confined in a box. We can then directly observe the wave patterns that start to occur and understand their interactions.

And then this: “Music itself is made of simple things – a reed, a pipe, a string. The great cosmic mechanisms are stupendous in their simplicity.” D’Arcy sure knew his way around words.

Simplifying also heavily increases our understanding of the principles of life, the universe and everything. When you think about it, it is used so often, you hardly even notice that certain simplifications have been made. D’Arcy points this out as well:

The stock-in-trade of mathematical physics, in all the subjects with which that science deals, is for the most part made up of simple, or simplified, cases of phenomena which in their actual and concrete manifestations are usual too complex for mathematical analysis; hence, even in physics, the full mechanical explanation is seldom if ever more than the “cadre idéal” towards which our never-finished picture extends. (4)

When considering biological systems, he states the following:

The fact that the germ-cell develops into a very complex structure is no absolute proof that the cell itself is structurally a very complicated mechanism: nor yet does it prove, though this is somewhat less obvious, that the forces at work or latent within it are especially numerous and complex. If we blow into a bowl of soapsuds and raised a great mass of many-hued and variously shaped bubbles, if we explode a rocket and watch the regular and beautiful configurations of its falling streamers, if we consider the wonders of a limestone cavern which a filtering stream has filled with stalactites, we soon perceive that in all these cases we have begun with an initial system of very slight complexity, whose structure in no way foreshadowed the result, and whose comparatively simple intrinsic forces only play their part by complex interaction with the equally simple forces of the surrounding medium. (5)

For many biological and non-biological systems, the initial conditions might not seem complex. It is by interactions between other – perhaps on their own relatively simple – environmental conditions, other simple systems, that it grows out to be complex. Obviously, as in the definition. But a complex system is more difficult to understand conceptually, more difficult to model. And that brings us the value of simplification, looking at smaller, simpler systems that more closely resemble the “cadre idéal”, allow us to pick apart the different players in a larger system. If we understand their individual behaviour, perhaps this can shed light on the collective behaviour.

As we analyse a thing into its parts or into its properties, we tend to magnify these, to exaggerate their apparent independence, and to hide from ourselves (at least for a time) the essential integrity and individuality of the composite whole. We divide the body into its organs, the skeleton into its bones, as in very much the same fashion we make a subjective analysis of the mind, according to the teachings of psychology, into component factors: but we know very well that the judgment and knowledge, courage or gentleness, love or fear, have no separate existence, but are somehow mere manifestations, or imaginary coefficients, of a most complex integral. (6)

As far as D’Arcy goes in his book, his simplifications hold true:

And so far as we have gone, and so far as we can discern, we see no sign of the guiding principles failing us, or of the simple laws ceasing to hold good. (7)

Of course, this does not automatically lead to complete understanding. We only get that tiny bit closer to seeing the bigger – and smaller – picture:

We learn and learn, but will never know all, about the smallest, humblest, thing. (8)

Because we must never forget that adding together those simplifications does not automatically lead to the answer to the complete problem (and I find this oddly poetic):

The biologist, as well as the philosopher, learns to recognise that the whole is not merely the sum of its parts. It is this, and much more than this. (9)

To end, D’Arcy also makes note of things beyond his comprehension:

It may be that all the laws of energy, and all the properties of matter, and all the chemistry of all the colloids are as powerless to explain the body as they are impotent to comprehend the soul. For my part, I think it is not so. (10)

---

Sources:

(1) Dr. George Martine, Medical essays and Observations, Edinburgh, 1747.

(2) On Growth and Form, p. 19
(3) On Growth and Form, p. 292
(4) On Growth and Form, p.  643-644
(5) On Growth and Form, p. 289
(6) On Growth and Form, p1018
(7) On Growth and Form, p. 644
(8) On Growth and Form, p. 19
(9) On Growth and Form, p1019
(10) On Growth and Form, p. 13
(2-10) from D’Arcy Thompson, On Growth and Form,  Cambridge university press, 1992 (unaltered from 1942 edition)

As you may well know, because you have read it here or heard it elsewhere, this year is the 100 year anniversary of D’Arcy Thompson’s On Growth and Form. The book is over 1000 pages long, and while extremely interesting, it can be quite a task to get through. Therefore, I figured I’d share some of the thoughts I had while reading – and to be honest, this was sometimes diagonally – through this masterwork.

To place this and future posts within context, I will first focus on how its main premise (physical forces as the driver of morphology) fits into the context of the time where the general sentiment was:

No other explanation of living forms is allowed than heredity, and any which is founded on another basis much be rejected… (1)

But that is not to say that no one in the scientific community was open to the idea that physics had some part to play:

To think that heredity will build organic beings without mechanical means is a piece of unscientific mysticism. (1)

It seems D’Arcy Thompson’s book was the first major publication on this idea, and his book is an inspiration for biomathematicians and biophysicists today. Or at least it is thought-provoking: throughout the book he underlines through several – 1000 pages worth of –  analogous observations from the material (non-living) and biological (living) world his theory, that the way biological systems grow, and the shape and size they eventually take, is driven by physical principles:

Cell and tissue, shell and bone, leaf and flower, are so many portions of matter, and it is in obedience to the laws of physics that their particles have been moved, moulded and conformed. … Their problems of form are in the first instance mathematical problems, their problems of growth are essentially physical problems. (2)

It is important to point out that he never claimed that physics is the only driving force of the shape and size of living things, just that it is one of the drivers, and that heredity is extremely important in understanding the processes of biology in its own right. But if outlining the physics of growth and form takes over a thousand pages, we should almost be thankful that heredity was taken out of the picture:

We rule “heredity” or any such concept out of our present account, however true, however important, however indispensable in another setting of the story, such a concept may be. (3)

Ruling it out of the picture doesn’t stop D’Arcy from occasionally musing on the limitations of heredity:

That things not only alter but improve is an article of faith, and the boldest of evolutionary conceptions. How far it be true were very hard to say; but I for one imagine that a pterodactyl flew no less well than does an albatross, and that Old Red Sandstone fishes swam as well and easily as the fishes of our own seas. (4)

This goes to show that while D’Arcy did not consider evolutionary theory in his story, it was not something he hadn’t thought about. He regularly quotes Darwin (I’m working through The Origin of Species myself at the moment… at least D’Arcy’s book had some pictures!) and as a professor in zoology, it stands to reason that he was knowledgeable on the subject.  Throughout his career, he published around 300 articles and books, and some day I’ll go through all of them to show he has written more on heredity.

To conclude, while On Growth and Form outlines an alternative theory to explain the morphology of biological systems, it is in no way trying to replace or contradict the theory of evolution or any idea of genetics-driven development. I’ll wrap up with one of D’Arcy’s final thoughts:

And though I have tried throughout this book to lay the emphasis on the direct action of causes other than heredity, in short to circumscribe the employment of the latter as a working hypothesis in morphology, there can still be no question whatsoever that heredity is a vastly important as well as a mysterious thing; it is one of the great factors in biology, however we may attempt to figure to ourselves, or howsoever we may fail even to imagine, its underlying physical explanation.  (5)

Well, that’s all folks. More on growing and forming next time! Have I mentioned that this book is over a thousand pages long?

---

Sources:

(1) Haller, 1888

(2) On Growth and Form, p. 10

(3) On Growth and Form, p. 284

(4) On Growth and Form, p. 873

(5) On Growth and Form, p. 1023

(2-5) from D’Arcy Thompson, On Growth and Form,  Cambridge university press, 1992 (unaltered from 1942 edition)

Last week’s University of Dundee podcast dealt on D’Arcy Thompson, so if you have 7 minutes to spare, listen to this:
https://www.dundee.ac.uk/50/podcasts/professor-biology/?utm_content=buffer8aeb9&utm_medium=social&utm_source=twitter.com&utm_campaign=buffer
Can you blame me to be inspired? #WhatAMan

Exactly a century ago, D’Arcy Thompson published his book On Growth and Form.

I’ve spoken about Mr. D’Arcy before, but as it is the 100-year anniversary of his masterwork, I feel it fitting to revisit the topic. Since mentioning him last, I have finished reading his book, and have also started to write up my thesis. I bring up my thesis because my work is related to D’Arcy’s work in the sense that I have been trying to bridge the gap between biology and physics, and I predict that some of my reading will inspire me to write more (hopefully more of my thesis but presumably also more on the general topic of bio-meets-phys).

Mr. D’Arcy wrote On Growth and Form to collect his observations on the mathematical principles of nature. He explains how biological phenomena of form and growth closely resemble physical and mathematical principles. Especially for some of the more simple examples (e.g. the shape and size of single or doublets of cells) the similarities between biology and physics (e.g. single and doublets of bubbles) are almost uncanny. These simple systems can easily be described using simple formulas, and he suggests that even more complex systems can be explained in a similar way (though he remarks that it will take a lot of formulas and paper space, luckily we have computers now). In 1917, this idea was pioneering, to say the least. Bio-mathematics and biophysics were nowhere near being the hot topics they are today.

One of the events organised for the anniversary of On Growth and Form, was the exhibition A Sketch of the Universe at the  City Art Gallery in Edinburgh, showcasing works of art that were inspired by the book, or by the idea that mathematics and biology are closely intertwined. The exhibition is closed now, but this weekend I did get the chance to go visit it.
So, I present to you, some of the highlights that I found interesting or cool-looking:

“I know that in the study of material things number, order and position are threefold clue to the exact knowledge; and that these three, in the mathematician’s hands, furnish the first outlines for a sketch of the Universe.” (D’Arcy Thompson, On Growth and Form)

“For the harmony of the world is made manifest in Form and Number, and the heart and the soul and all the poetry of Natural Philosophy are ebmodied in the concept of mathematical beauty.” (D’Arcy Thompson, On Growth and Form)

“The waves of the sea, the little ripples of the shore, the sweeping curve of the sandy bay between the headlands, the outline of the hills, the shape of the clouds, all these are so many riddles of form, so many problems of morphology.” (D’Arcy Thompson, On Growth and Form)

You can read more about D’Arcy Thompson, On Growth and Form and some of the events being organised this year in honour of the 100 year anniversary, here. And presumably in the near future on this very blog.

[Note: Again, I realise that D’Arcy Thompson’s last name is “Thompson” so “Mr. Thompson” would be a more appropriate title (or Prof. Thompson) but I just cannot resist his practically Austenesque first name.]

Before I start, a short comment on personal growth:
After a quite frustrating day yesterday, I decided to get up bright and early, go for a run and then head to work today. It’s actually a national holiday here (Ascension), but as I have to take my holidays explicitly, and “I’m here for work and not for fun (except for weekends)”, that was my plan. So I was up and ready to leave for my jog, when my flatmate just entered the front door, after a night out. Made me think.
I guess I’m a “real grown-up” now…
But now, On Growth and Form.
I have discovered that Dundee has had quite an interesting inhabitant. His name is D’Arcy Wentworth Thompson. I had never heard of him until sometime last year when we went out to dinner in a restaurant called The D’Arcy Thompson. A plaque on the wall informed us he was a biology professor in Dundee (at the time the university was still part of the University of St. Andrews) around 1900.
Sometime later, I went to a talk about penguins, more specifically about the two penguins that Dundonian Arctic explorers had brought back from their trip south. The penguins had gone through quite a bit, one even was the official mascot of a student faculty club, but they are now on display in the D’Arcy Thompson Zoology Museum on the campus of the University of Dundee. We went to go see the museum after the talk, it’s a room stuffed with, well, stuffed animals. Quite an impressive collection, including a giant crab. (Giant means more than a meter across. Imagine running into a wild one!)

But it wasn’t until last week that I realised how interesting Mister D’Arcy really was – and I just realised that sounds like a sentence from Pride and Prejudice. A research letter in Nature Physics on the combined mechanics of cells in tissues mentions the following:

In 1917, D’Arcy Thomson published a treatise On Growth and Form in which he suggested that morphogenesis could be explained by forces and motion – in other words by mechanics.

You might recall that my PhD is about the mechanics of gut cancer. And I didn’t know about D’Arcy, shame on me! In the meantime I’ve tried to get my hands on the book, not too difficult because there are some on line pdfs circulating with the whole thing. Unfortunately, I’m the worst at reading from a computer screen, so I haven’t gotten very far*, but it seems that Mister D’Arcy was quite interesting indeed. His 1136-paged book reads a bit a philosophy book (or it does in the first 304 pages). He tells the story – for it’s written like a story – of how the mechanics in biology is quite similar to the mechanics of inanimate bodies, and that growth and morphology can essentially be explained by physics. He gives a whole list of examples, where he makes analogies between biological systems and physical systems. He admits that this will not explain every detail of biology, but that it is possible to explain certain simpler phenomena of organic growth and form using mathematical and physical descriptions. His studies on fractal patterns and linear transformations (rotation, translation, shearing) have been important for image analysis, architecture, mathematics and probably many other fields.

Then how had I never heard of Mister D’Arcy (I realise it should be Mister Thompson but that just doesn’t have that ring to it)? Luckily I’ve figured my lack of knowledge on time and can rectify that mistake. D’Arcy had innovative ideas, that have been pushed to the sidelines by molecular and genetic research in morphogenesis. Nevertheless, is book is merely descriptive, so there is still much to be learned. Which is where projects like mine come in.
Hurray, I have a purpose!

*If anyone knows where I can get my hands on a good hard copy, please let me know! Amazon only cells “bad quality and incomplete” versions, so it’s proving quite difficult.